DEV...ELeferno

Dnešní téma považuji za nejkontroverznější a studenty medicíny v rámci výuky diagnostických metod obvykle nejméně oblíbené. Složení (a dosavadní reakce) čtenářů Eleferna mi ale skýtají jistou záruku, že si tuto relativně obtížnou a veskrze teoretickou část výkladů osvojí snadno a s prospěchem pro vlastní rozvoj. Za úspěšné bych považoval, pokud by měl čtenář po pročtení (a nezastírám, že místy i opakovaném) tohoto článku jasno v tom, jak se zobrazuje elektrická srdeční aktivita a jakými způsoby ji lze sejmout a zaregistrovat. Současně by si čtenář měl bez většího úsilí osvojit pojem elektrické osy srdeční a elektrického srdečního vektoru a měl by v teoretické rovině umět použít základní schémata snímání EKG, včetně pojmenování a umístění svodů.

Jak bylo vysvětleno v předchozím výkladu, lze na elektrickou aktivitu srdce pohlížet jako na sumární superpozici elektrických aktivit jednotlivých myomů. Jako mezistupeň lze (a v rámci některých invazvních vyšetření je to i účelné) vydělit dílčí elektrické aktvity jednotlivých srdečních struktur, z nichž je - opět superpozicí - složena výsledná elektrická srdeční aktivita. Ta se mění v rámci srdečního rytmu mění jak v čase, tak v prostoru - jinými slovy řečeno, mezi různě umístěnými elektrodami naměříme různě vyhlížející EKG křivky. Proto je mimořádně důležité, aby si čtenář ujasnil mechanismus, jakým je vytvářen formalisovaný popis elektrické aktivity srdce a na jakých fyzikálně opodstatněných základech je postaven.

Prvním a základním předpokladem, z něhož vychází veškerá elektrokardiorafie je předpoklad lineárního modelu - superpozice. Jinými slovy předpoklad říká, že na aktivitu srdce jako celku můžeme v daném časovém okamžiku pohlížet jako na jediný elektrický srdeční vektor, proměnný v čase i prostoru. Ráz proměnlivosti v čase má přitom charakter nepravidelné rotace za současné změny jeho absolutní velikosti. Jednotlivým vlnám a komplexům EKG křivky pak lze přiřadit dílčí osy, zvané osy vln. Jde o "zmrazení" polohy elektrického srdečního vektoru v časovém okamžiku, odpovídajícím maximu amplitudy vlny. Často užívány jsou hlavně osy vln P a T a osa komplexu QRS. Ta je - není-li výslovně stanoveno jinak - považována za hlavní osu a je označována jako elektrická osa srdeční. Je důležité uvědomit si na tomto místě, že zmíněné osy jsou projevy způsobu šíření vzruchu tkáněmi a elektrické aktivity srdečních struktur a tudíž nezávisí na bezprostředně na fyzické orientaci myokardu.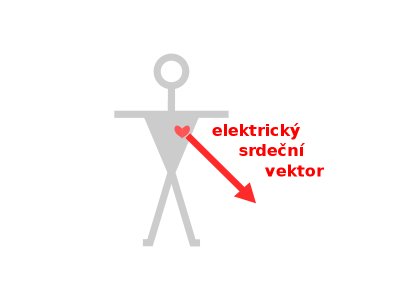

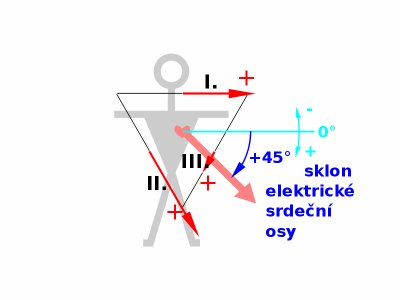
Ve frontální rovině směřuje hlavní srdeční osa šikmo vlevo dolů v širokém rozmezí sklonu od nuly do cca 100°. Směr kladného přírůstku úhlu je přitom v kardiologii přijat opačně, než v geometrii, tedy úhel vzrůstá rotací po směru hodinových ručiček.  Poloha hlavní srdeční osy se mění i s věkem pacienta, většinou posunem směrem k záporným hodnotám, u populace po pětačtyřicátém roce života se osa posouvá do rozsahu od cca -30°do 90°. Významné posuny indikované osy mohou zapřičinit zejména (a v praxi nejčastěji) začátečnické chyby v umístění elektrod, patologicky pak hypertofie či dilatace srdečních komor a bloky Tawarových ramének. Doprava vychýlená osa přitom ukazuje na hypertofii pravé komory srdeční či zadního raménka, osa vychýlená doleva ukazuje postižení levé komory či blok předního raménka. Téma bude podrobně osvětleno v samostatné výkladové části, věnované diagnostice.

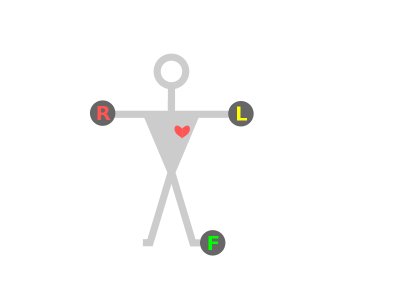
Dalším základním předpokladem, nutným k následujícímu výkladu je stanovení rovin, v nichž elektrický srdeční vektor vyšetřujeme. Vektor, jak bylo řečeno výše, vykonává složitý pohyb v trojrozměrném prostoru. Diagnostické metody EKG v naprosté většině případů na komplexicitu trojrozměrného vyšetření rezignutí a v rámci zjednodušení pracují s rovinnými průměty do planizovaného povrchu těla pacientova. Tohoto předpokladu využil již zakladatel moderní elektrokardiografie W. Einthoven, který zavedl jako základní způsob vyšetření snímání projekce srdečního vektoru ve frontální rovině trojicí elektrod. Ty jsou umístěny na povrchu pacientova těla, které pro účely vyšetření považujeme za homogenní elektrolytický vodič. Einthovenovo vyšetření bylo založeno na lokalizaci elektrod na pravé a levé ruce a levé noze, v ideálním případě jsou pak elektrody umístěny v úhlech 120°tak, že srdce (považované za bodový objekt) je ve vrcholu těchto úhlů. V elektrokardiografii je přijato ustálené označení jednotlivých elektrod písmeny (někdy s číselným indexem), přičemž jednotlivým elektrodám jsou přiřazeny i barvy pro snazší umisťování elektrod i méně kvalifikovaným personálem. Téma  bude podrobněji rozvedeno dále, zde je nutno pouze uvést, že tři Einthovenovy základní elektrody jsou označovány jako R (na pravou ruku, červená), L (na levou ruku, žlutá) a F (levá noha, zelená).

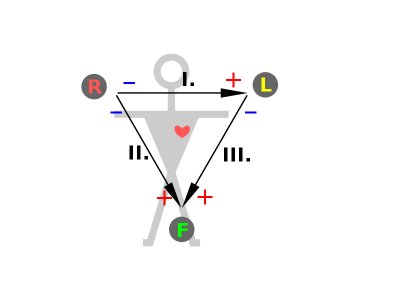
Výše popsaná trojice svodů tvoří takzvaný Einthovenův trojúhelník. V rámci zjednodušení považujeme tento trojúhelník (bez ohledu na skutečné umístění elektrod) za rovnostranný, tedy s identickými vrcholovými úhly 60°. Mezi jednotlivými dvojicemi elektrod můžeme získat tři různá napětí, označovaná v elektrokardiografii jako Einhovenovy svody. Ty jsou definovány takto:

•  I.=L-R
• II.=F-R
• III.=F-L

Tato forma zápisu označuje, že například svod I. je definován jako rozdíl potenciálů mezi elektrodami L a R, jak ukazuje obrázek. Dohoda o znaménkách zobrazení pak říká, že kladnému směru křivky (nahoru) odpovídá zvyšující se potenciál L, zápornému směru (tedy dolů) pak zvyšující se potenciál R. Čtenářům s elektronickou či elektrotechnickou praxí se toto označení může zdát matoucí (používají přesně opačného), nicméně jde o dobou ustálený a bezvýhradně užívaný úzus. Einhovenovy svody jsou tvořeny rozdílem dvojice potenciálů, označujeme je proto jako svody bipolární. Šipky, která je označují lze interpretovat jako vektory a nadále s nimi manipulovat dle pravidel pro vektorovou algebru.

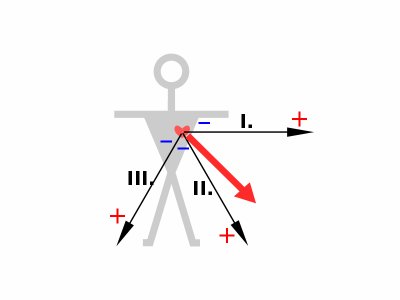
Pro praktické účely je vhodné, aby vektory trojice Einhovenových svodů byly orientovány vzhledem k srdci. Ve frontální rovině je proto přesuneme (legální transformace) tak, aby všechny vektory vycházely ze středu srdečního svalu.

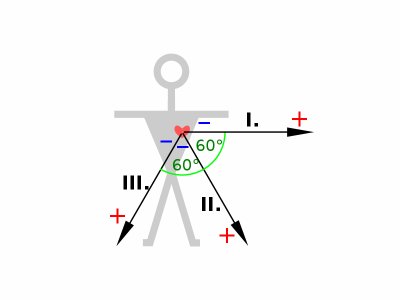
Získáme tak (nekartézskou) soustavu os specifického souřadného systému se sklonem os 60°. V této souřadné soustavě pak vyšetříme umístění elektrického srdečního vektoru (typicky vektoru komplexu QRS, jak bylo vysvětleno výše). Za tímto účelem rozložíme elektrický srdeční vektor do námi vytvořeného souřadného systému. Stejně, jako v kartézské soustavě provedemem kolmé průměty vektoru do souřadných os, čímž vymezíme dílčí napětí na svodech, odpovídající dané poloze vektoru v konkrétním okamžiku. Zde uvedený postup byl použit jako metodicky i didakticky pohodlnější - v  praxi se ovšem setkáváme s opačnou úlohou, kdy známe (naměřená) napětí na svodech, z nichž rekonstruujeme polohu vektoru srdeční osy. Postup je logický - na jednotlivé osy vyneseme odpovídající hodnoty naměřených napětí a průsečíkem kolmic, vedených k osám v těchto místech již snadno zjistíme vrchol hledaného vektoru.   

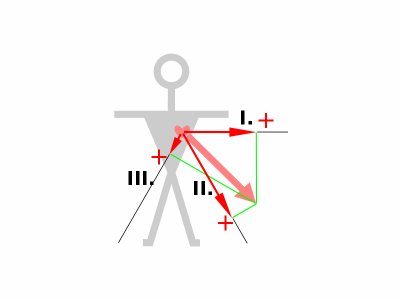
Dále - pro účely dalšího výkladu a zavedení nových pojmů - přesuňme legální transformací souřadné osy tak, aby opět tvořily trojúhelník. I v takovémto trojúhelníku bude možno provádět výše uvedené operace, tedy rozklad i rekonstrukci elektrického srdečního vektoru, bez ohledu na pozici, do které trojúhelník umístíme.

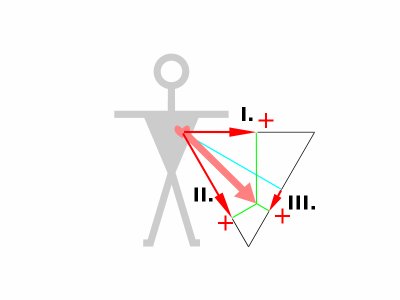
Umístěme proto trojúhelník tak, aby počátek vektoru odpovídal poloze srdce. Takovýto trojúhelník pak nazýváme trojúhelníkem centrovaným. V takovémto trojúhelníku pak všechny QRS komplexy směřují směrem nahoru - vlna R je vyšší, než průměr potenciálů vln Q spolu s S.    

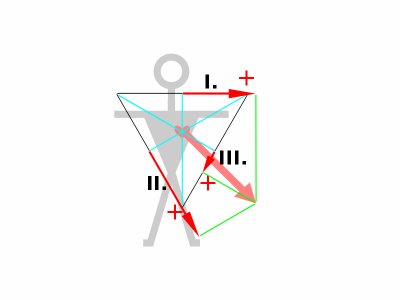
V centrovaném trojúhelníku je velmi snadné stanovení sklonu elektrické srdeční osy. Pokud je vyšetřovaný vektor vektorem srdeční osy (okamžik maximální amplitudy vln P, R nebo T), zjistíme sklon odpovídající osy jako úhel vektoru a vodorovné osy s tím, že jak bylo vysvětleno výše, kladný směr růstu hodnoty úhlu je opačný, než v geometrii. Nulový úhel odpovídá směru elektrody L a kladný přírůstek odpovídá směru k elektrodě F.

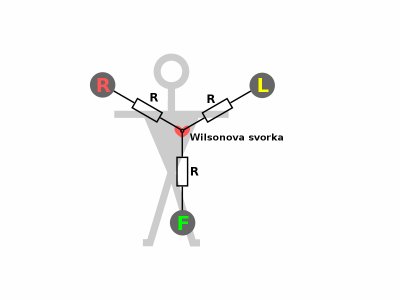
Einthovenovy svody jsou, jak již bylo výše uvedeno, svody bipolární. V některých případech je potřebné, aby byl svod definován vůči jedinému refenčnímu bodu. Potřeba je dána zejména instrumentálními požadavky, spojenými s realizací snímacích zesilovačů. Jako referenční bod je často používán bod s průměrným potenciálem elektrod R, L a F, instrumentálně realizovaný trojicí identických rezistorů, spojujících elektrody se společným uzlem, zvaným Wilsonova svorka.

Svody, vzniklé mezi Wilsonovou svorkou a elektrodami pak nazýváme svody Wilsonovými a označujeme je jako VR, VL a VF. Takto definované svody označujeme jako unipolární. Jejich potenciál snadno odvodíme z potenciálů elektrod R, R a F takto:
Z definice je potenciál Wilsonovy svorky W roven W=(R+L+F)/3. Pak platí že

• VR = R - W = (2R-L-F)/3
• VL = L - W = (2L-R-F)/3
• VF = F - W = (2F-L-R)/3

V grafickém vyjádření lze Wilsonovy svody zakreslit jako trojici vektorů, vycházejících z Wilsonovy svorky do vrcholů, reprezentujících jednotlivé elektrody. S nimi lze zacházet podobně, jako s vektory svodů Einthovenových, vůči nimž jsou Wilsonovy vektory pootočeny o 30°. Získáváme tak systém šesti os, reprezentujících trojici bipolárních a trojici unipolárních svodů.

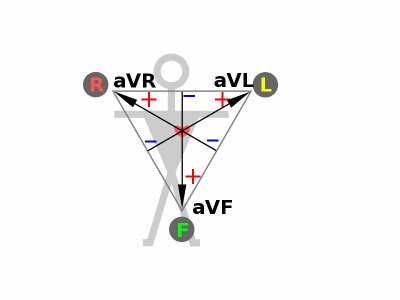
Fyzická realizace Wilsonových svodů vede (jak si čtenář z geometrie snadno odvodí) k významně redukované délce jim odpovídajícíh vektorů a tedy i menšímu nasnímanému napětí. Problémem se zabýval Goldberg, kterému se počátkem čtyřicátých let podařilo zvýšit voltáž svodů tím, že referenční body přemístil odporovou sítí ze středu do protilehlé strany trojúhelníka.

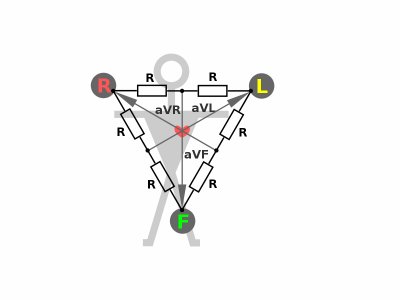
Takovéto napětí je o 50% vyšší, než napětí Wilsonovo. Tyto svody označujeme jako augmentované, tedy prodloužené a označujeme je jako aVR, AVL a aVF. Z definice je potenciál referenčního bodu Goldberova svodu roven průměru potenciálů zbývajících elektrod. Platí tedy, že

• aVR = (2R - L - F)/2
• aVL = (2L - R - F)/2
• aVF = (2F - R - L)/2

Porovnáním se vztahy pro Wilsonovy svody snadno ověříme, že napětí augmentovaných svodů tvoří 3/2 napětí svodů Goldbergových. Tím jsme zakončili poměrně obtížné téma elektrické vztažné soustavy srdce (ještě jej rozvedeme v příští části doplněním o další svody) a můžeme se začít věnovat již praktické instrumentaci.

Při přípravě tohoto textu byly využity materiály nadace Wikimedia ve zpracování Petra Heřmana (aka Kychota). Tento text je dále šiřitelný pod licencí Creative Commons 3.0 unported.